2024-编译原理-词法篇

1 编译原理简介

### 1.1 编译器的工作

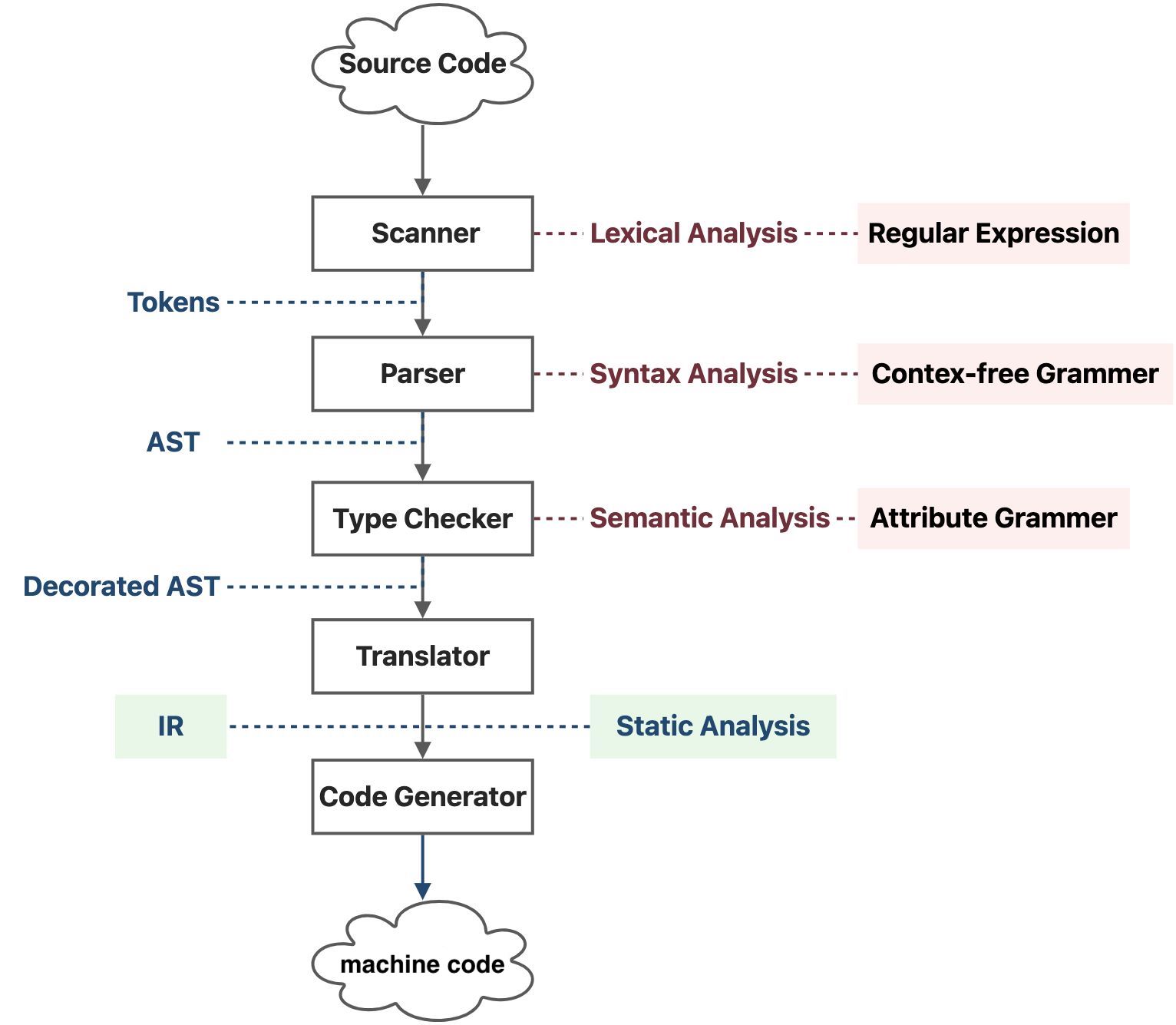
词法分析（Lexical Analysis）
语法分析（Syntax Analysis / Parsing）
语义分析（Semantic Analysis）
中间代码生成（Translating）
优化（Optimization）
代码生成（Code Generating）

1.2 关于IR

IR：Intermediate Representation，中间表示，由编译器前端产生，被后端使用。
- 树型IR：如语法分析树、抽象语法树。
- 线性IR：如三地址码。
为什么要有IR？
1. 统一编译成中间表示，从而分离开前端和后端，降低耦合
2. 方便机器无关优化（大量的优化 / 分析都在IR上进行）

1.3 串和语言

1.3.1 基本概念

字母表，一个有限的符号集合；
串，字母表中符号组成的一个有穷序列；
语言，给定字母表上一个任意可数的串的集合；
前缀 / 后缀 / 子串
真前缀 / 真后缀 / 真子串
空串，

1.3.2 串的运算

连接：如
幂次：如
翻转：如
长度：如

1.3.3 语言的运算

语言本质上是一个集合，所以语言可以进行通用的集合运算如：交、并、差、补
语言的翻转：
语言的连接：
语言的幂乘：
- (共个)；
星闭包：
正闭包：
例子：

表示什么？

表示什么？

1.4 P vs NP

P问题 —— 确定性算法在关于输入规模的多项式时间内可解
NP问题 —— 非确定性算法在关于输入规模的多项式时间内可解

2 词法分析的理论基础

2.1 正则表达式

正则表达式（Regular Expression, RE）是词法分析使用的工具。
正则表达式以代数形式描述了一个语言。（准确的说，是一个正则语言）

2.1.1 定义

定义 正则表达式 如下：

基础情况：

如果是一个符号，那么是一个正则表达式，且。
是一个正则表达式，且。
是一个正则表达式，且。

递归情况：

如果与是正则表达式，那么也是一个正则表达式，且。（并）
如果与是正则表达式，那么也是一个正则表达式，且。（连接）
如果是一个正则表达式，那么也是一个正则表达式，且。（星闭包）

2.2.2 运算符优先级

星闭包 > 拼接 > 并

2.2 有穷自动机 (Automaton)

两种有穷自动机：
- DFA (Deterministic Finite Automaton)， 确定性有穷状态自动机
- NFA (Nondeterministic Finite Automaton)， 非确定性有穷状态自动机
有穷自动机是一种能记忆有限量信息的形式系统，可用于接受或拒绝某一个特定的字符串，有穷自动机所有接受的字符串的集合就是它所定义的语言。
有穷自动机的关键是状态和转移

2.2.1 DFA和NFA的定义

这种逐一描述被定义对象的各个元素的形式化定义方式叫作 “声明式定义”

NFA 是一个五元组：
1. 字母表（）
2. 有穷的状态集合
3. 唯一的初始状态
4. 状态转移函数
5. 接受状态集合
  - 接受状态也称为终止状态，一般在状态转换图中用双圈表示
DFA 是一个五元组：
1. 字母表（）
2. 有穷的状态集合
3. 唯一的初始状态
4. 状态转移函数
5. 接受状态集合

2.2.2 DFA和NFA的区别

DFA的特点：
- 一个字符只能转移到唯一确定的下一个状态。
- 不支持空串转移。
NFA的特点：
- 当前状态下，在一个字符的驱动下可以转移到两个（或多个）不同状态。
- 允许使用转移，即没有任何字符驱动也有可能转移。
二者区别：
- DFA容易被计算机实现，但人类理解它较困难。
- NFA 描述一个语言更容易被读懂；但是不用于实现词法分析器。

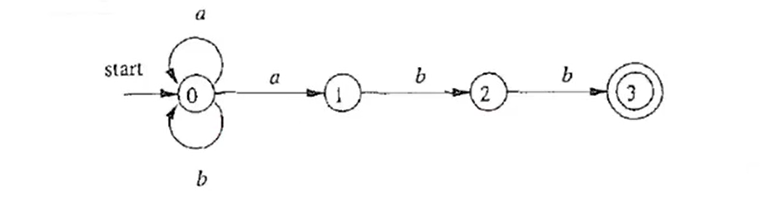
2.2.3 状态转换图

通常，我们用一张直观的图来表示有穷自动机，这就是状态转换图。

示例：

2.2.4 DFA、NFA、RE的等价性

DFA、NFA和RE都能够定义语言，那么它们所定义的语言之间会有什么关系吗？

2.2.4.1 重要的转换图

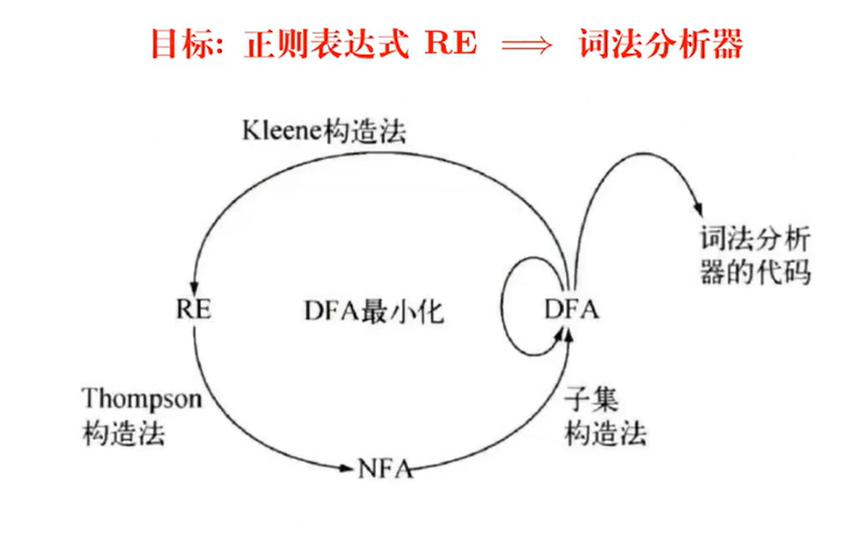
RE 到 NFA
- Thompson 构造法
NFA 到 DFA
- 子集构造法
DFA到 DFA 的自环
- DFA 最小化
- Hopcroft算法
DFA 到 RE
- Kleene 构造法

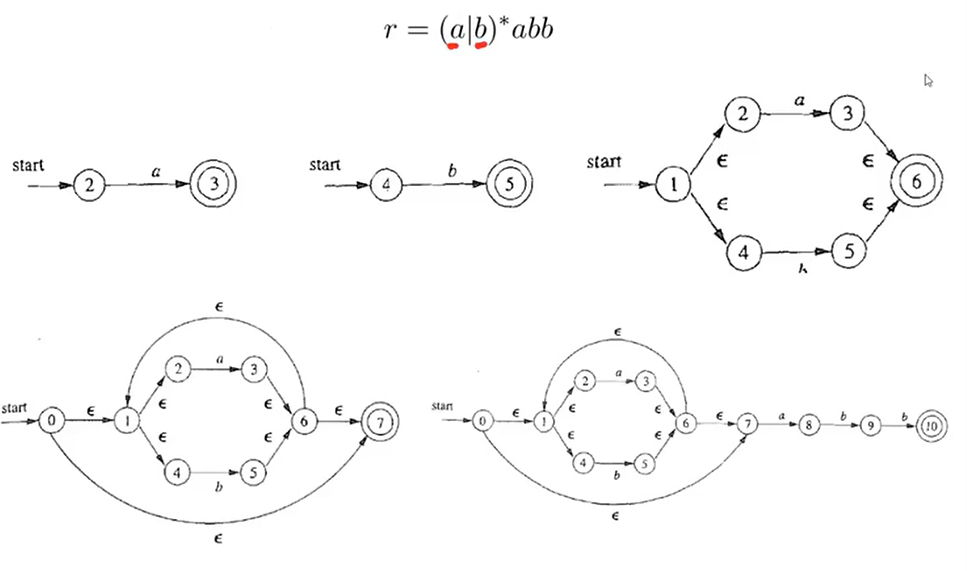
2.2.4.2 RE 到 NFA （Thompson 构造法）

基本思想：按结构归纳。

是正则表达式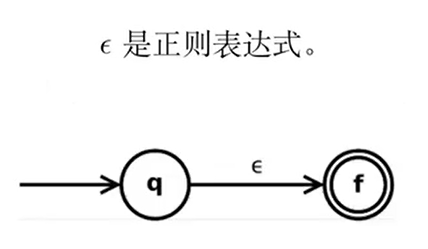
是正则表达式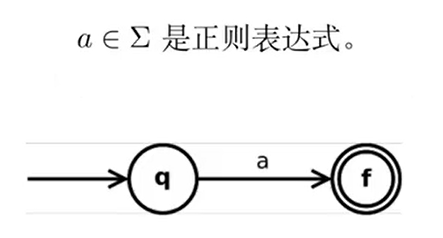

如果是正则表达式，则是正则表达式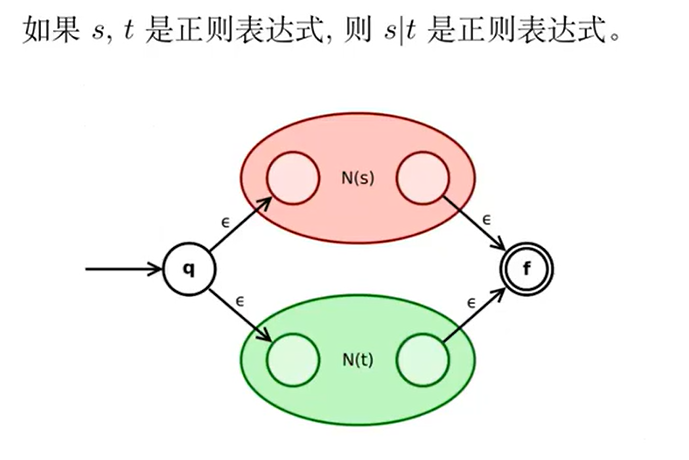
如果是正则表达式，则是正则表达式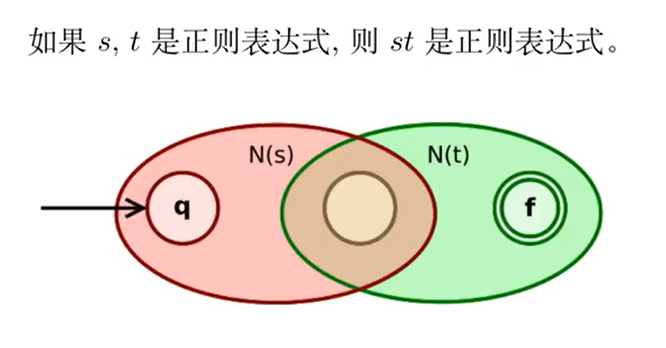
如果是正则表达式，则是正则表达式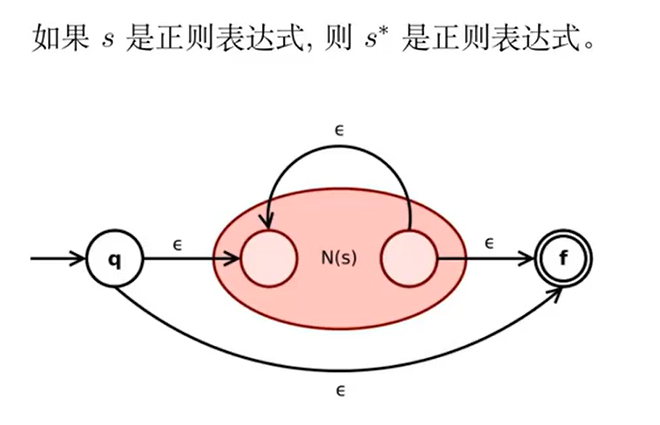
例子：

2.2.4.3 NFA 到 DFA （子集构造法）

思想：用 DFA 模拟 NFA。通过不断模拟走一步，来合并所有等价的状态。
子集构造法形式化描述：

考虑一个NFA，具有状态集，字母表，转移函数，初始状态，终止状态集。

构建一个等价的DFA ，具有状态集，字母表，初始状态，终止状态集

这里需要注意的关键点是，DFA的状态集中的元素是NFA中状态的集合。也就是说，作为一个DFA的状态，应当视为一个DFA状态集中的一个元素，给该状态起名为，但是仍然是一个状态。

定义转移函数为：

这里的返回值对于NFA来说是一些状态的集合，不过对于DFA来说只不过是一个状态而已
子集构造法算法步骤：
1. 确定 DFA 的初始状态，即为指向的状态（）以及经过转移能到达的状态构成的集合。
2. 遍历当前状态下的所有可能的输入字符，寻找经过转移之后能到达的状态集。
3. 将经过转移后可到达的状态集作为 DFA 的一个新状态，并构造从当前 DFA 状态到这一新状态的状态转移。
4. 将上一步的新状态作为当前状态，返回第2步，重复操作，直至无法再构造出新的DFA状态
5. 标注接受状态：NFA 的接受状态所在的那些 DFA 状态集就是接受状态。
复杂度分析：
- NFA的状态数:
- DFA的状态数:
- 仅为理论结果，实际上常见的程序设计语言中，DFA和NFA的状态数大致相同。

2.2.4.4 DFA最小化

最小化DFA的状态数可以提升计算效率，对于设计词法分析器很有意义。
Hopcroft算法
- 核心思想：等价的状态可以合并。
等价状态的定义
- 等价的状态通过相同转移到达的状态还是等价，不等价状态同理。
如何找到等价的状态？
- 先假设所有的状态整体为一个等价类，然后根据一定规则将不等价的状态划分到不同的等价类中。
- 初始时，所有的接受状态和所有非接受状态天然不等价，故作为状态集合的初始划分。
算法步骤：
1. 将所有状态进行初始划分，（为接受状态）。
2. 遍历所有可能的输入，根据之前对于等价状态的定义，如果该输入导致本来处于相同等价类的状态和转移到了不同的等价类中，则进行一次划分，将和所在的等价类分为两份，令和落入不同的等价类（此时可以认为将这两个状态区分开了），如此重复，直到再也无法对任何等价类进行划分（到达不动点）。
3. 剩下的同一等价类里若有多个状态，则它们就是等价状态，将它们合并。
思考：按照上面的算法，同一个DFA可能会被构造出多个不同构的最小DFA吗？
- 不可能。
- 反证法，假设有两个状态数不相等的由Hopcroft算法得到的最小DFA 和，不失一般性，假设状态数更少，由上述的算法可知的每个状态皆是一个等价状态。考虑利用Hopcroft算法的第2步，在和之间构建等价类，则由于鸽笼原理，必然会有至少2个的状态与的某个状态等价，如此的这两个状态可以合并，产生矛盾。
Hopcroft 算法的局限性：
1. 不适用于 NFA 最小化
2. 事实上，NFA 的最小化问题是 PSPACE-complete 的。（可理解为，目前还未找到该问题的一个确定性的多项式空间算法）

2.2.4.5 DFA到RE （选学）

（以下内容搬运自《形式语言与自动机》课程）

考虑使用数学归纳法，我们记的状态为，归纳是对于我们允许遍历的路径上面的最大状态数字进行的。
于是，我们要定义一下什么是k-路径 (k-path) 了。k-路径指的是DFA状态转换图上的某一条路径，其中，这条路径经过的所有状态的标号不超过。（1. 一定是经过，起点和终点不算 2. 中间“跳过”的节点（状态）的编号都要 <= k ）
所以我们可以明显地看到，所有的路径都是n-路径，因为最大的标号就是n了。 (找到了所有的n-path, 就找到了所有的接受的串)

而一个DFA对应的正则表达式就是所有的从起始状态到终止状态的n-路径的正则表达式的并。因为所有的n路径就组成了整个DFA。
下面我们来证明一下DFA可以转化成RE，也就是所有的n-路径都能转化成RE。这里我们不规定路径起点终点了，这样我们会证明一个更强的结论。

其实核心思路就是证明DFA上的路径都可以转化成正则表达式，而DFA表示语言就是通过路径的标号序列来表示的，从而所有的DFA都可以转化成RE了。

时，只能通过弧或者就留在自身。下面我们只需要证明，能够通过 -路径对应的正则表达式构造出 -路径对应的正则表达式即可。

令表示从状态走到状态的所有k-路径组成的语言的正则表达式。

基础情况：时，是所有的从到的弧上的标号的和。
- 如果没有弧的话，则；
- 如果的话，则在自环的基础上添加。
例如在上面的例子中，，。

归纳步骤：假设所有的 -路径都可以转化成正则表达式。

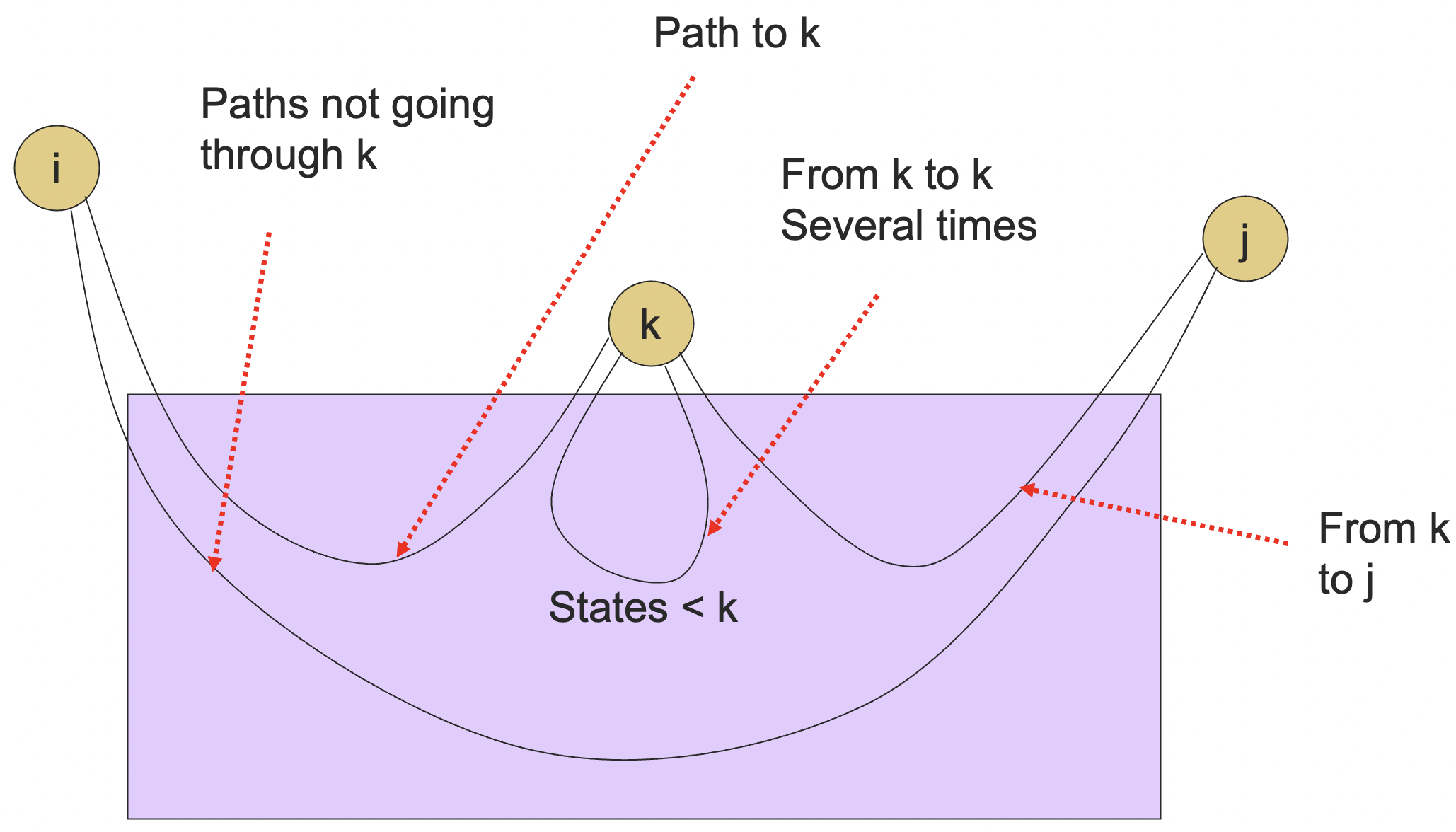
一条从到的k-路径要么从来没经过状态k，要么经过了状态k至少一次。

于是，我们有：

这个递归式中每一项的含义如下：
- 指的是不经过；
- 指的是第一次从走到；
- 指的是从走到 0次或者更多次；
- 指的是从走到。
图示如下：

又了上面的k-路径与RE的转化之后，一个DFA的RE就是所有的总和（并）了，其中：
- 是DFA的状态数，这样的话路径就没有任何限制了；
- 是初始状态；
- 是终止状态中的任意一个。

2.3 正则语言

至此，我们给出了DFA、NFA、RE所定义的语言之间互相转换的算法。从而也就证明了这三种形式系统所定义的语言竟然是同一类语言，称为“正则语言”。
正则语言非常规整，非常漂亮，具有很多很好的性质。

2.3.1 泵引理

正则语言的泵引理（Pumping Lemma），对于每一个正则语言来说，存在一个整数，使得对于中的每一个长度的字符串，我们可以写作，满足：

整数也称为泵引理常数。

2.3.2 泵引理的简单应用

泵引理是正则语言所具备的性质，即某个语言满足泵引理是其为正则语言的必要条件。
证明： 不是一个正则语言。

假设它是一个正则语言，那么根据泵引理，存在一个泵引理常数，考虑字符串，我们可以写作，其中，于是都是全0，于是中的比多，不在中，这与泵引理矛盾。
事实上，是一个上下文无关语言。

2.3.3 成员资格问题

对于给定正则表达式描述的语言，字符串在不在这个语言里？
一个可能的想法是，我们根据正则表达式生成一个与之等价的DFA，然后将在这个DFA中模拟执行，判断是否接受。
这件事实际上是就是词法分析。

3 词法分析

输入：源代码（字符流）+ 给定的词法规则

输出：词法单元（Token流）
什么是Token？一个Token包括Token类和具体属性，例如，<number, 60> 就是一个Token，表示一个数字，值为60.
词法分析阶段通常使用RE描述语言的词法，根据RE构造DFA，利用DFA的接受完成Token识别。
词法分析器的匹配原则：最长优先匹配。

其实现流程为：
1. DFA处于初始状态，开始读取输入并进行状态转移；
2. 若输入流已读取完，且为接受状态，则完成识别；
3. 否则，如果无法再继续读取，回溯至最近的一次接受状态，识别到一个Token，然后返回第1步；
4. 若没有经过任何接受状态，报错（输入不合法）。

4 ANTLR 4 简介

词法分析器的3种设计方法：
1. ANTLR等词法分析器生成工具
2. 手写
3. 自己实现词法分析生成器
为什么手写？

性能 / 其他设计 / 相对简单（语法分析器本课程不手写）
ANTLR

输入: 词法单元的规约 .g4 （g 的意思是 Grammar; 4 的意思是 ANTLR4）

输出: 词法分析器此处为一系列.java文件.
运行词法分析器, 输入为源程序, 得到输出即为词法单元（Token）流.
ANTLR 4的.g4语言用于设计另一门语言, 因此.g4语言称为元语言

.g4的一个例子

grammar SimpleExpr; // 必须和文件名同名

prog : stat* EOF; // 一个program是由0到任意多个(*)语句(stat)构成的, EOF -- 表示文件结束
stat : expr ';'  // 引号里面的;是正在设计的语言的一部分
	 | ID '=' expr ';'  // 备选分支
	 | 'print' expr ';'
	 ;
// 加减乘除表达式, 这一行本身是一个大的规则, 其中的括号并列4种运算符叫子规则 
expr : expr ('*' | '/') expr // g4文件里, 写在前面的运算优先级高
	 | expr ('+' | '-') expr
	 | '(' expr ')'
	 | ID
	 | INT
	 ; // 如果没有特别配置, 那么g4文件就默认运算符左结合

// 语法规则已写完, 以下是词法规则
ID : ('_' | [a-zA-Z]) ('_' | [a-zA-Z0-9])* ; // 正则表达式, []表示字符集合
INT : '0' | ('+' | '-')? [1-9][0-9]*;

SL_COMMENT: '//' .*? '\n' -> skip ; // 这里如果不加?就是贪婪匹配, 加?就是非贪婪匹配(所有匹配的可能性中, 选择最短的那个匹配)

WS : [ \t\r\n]+ -> skip; // 识别空白符, +表示一个或多个; -> skip表示丢掉这一词法单元, 不进入语法分析

最前优先匹配原则，当有多条规则可以匹配时，选择最前面的优先匹配。
fragment关键字

不参与实际识别，只是方便编写语法

例如: fragment LETTER : [a-zA-Z]，这个 LETTER 并不会被识别成词法单元。
1
2
3
fragment LETTER : [a-zA-Z] ;
fragment NUMBER : [0-9] ;
fragment WORD : '_' | LETTER | NUMBER ; // 这是个常用做法

~ 表示除了...以外的字符:

例子:

1	SL_COMMENT2 : '//' ~'\n'* '\n' -> skip ;

语法单元的规约要以小写字母开头, 词法单元以大写字母开头.
最长优先匹配原则:

1.23 为什么没有被匹配成 1和 .23呢？

因为匹配时尽可能地使得匹配程度最长。即只要还能匹配就要继续匹配，除非已经无法再匹配。
使用 lexer grammar ... 开头，表示此文件描述词法规则。