2024-编译原理-语法篇

1 语法分析的理论基础

1.1 上下文无关文法

• 上一讲中我们使用正则语言的泵引理（Pumping Lemma）证明了 并非正则语言。还有一些常见的语言，如回文串 也不是正则语言。
• 事实上，这两种语言都是上下文无关语言，它的表达能力严格强于正则语言。

1.1.1 简介

1. 文法（Grammar）用于描述一个语言。
2. 一个上下文无关文法（Context-Free Grammar，CFG）确定地形式化地描述了一个语言。（具体地，是一个上下文无关语言）
3. 关于Context-Free：
   • 有Context-Free（上下文无关）Grammar 也就有Context-Sensitive（上下文相关 / 上下文敏感）Grammar。
   • Context-Free Grammar的表达能力弱于Context-Sensitive Grammar。
   • 为什么在《编译原理》课程中我们只学习上下文无关文法？
   • 因为在实际几乎所有的现代编程语言的语法都是上下文无关的，因此使用CFG做语法分析就足够。

1.1.2 形式化定义

这也是一个声明式定义

• 定义 上下文无关文法（Context-Free Grammar） 为一个四元组 ，其中：

  • 是 CFG 所要定义的语言的字母表，称为 终结符(Terminals) ；

  • 是一个有限的其他符号的集合，每个符号代表了一个语言，称为 变量(Variables) 或者 非终结符(Nonterminals) ；

  • 是代表 CFG 所要定义的语言变量，称为 起始符号(Start Symbol) ；

  • 是 产生式（productions） （也译作：生成式 / 推导式） 的集合，表示语言的递归定义，每个产生式形如 ，其中：

    • 产生式头 (head) 是一个变量；

    • 产生式体 (body) 是变量和终结符组成的字符串，可以是空串。

• 符号约定：

  • 习惯上，使用大写字母 和 表示非终结符；而使用小写字母 来表示终结符。

• 例子：

  • () ，我们已知它不是正则语言，此时如果使用上下文无关文法描述它，就证明了它是上下文无关语言（上下文无关语言（CFL）是上下文无关文法（CFG）定义的语言）。
  • 做到这一点很简单, 令, , , 即可.

1.1.3 推导

1. 如果 是一个产生式，则称 为 推导（derive） 出 ，这样就定义了一步推导。

2. 迭代推导（iterated derivation）：表示经过零步或若干步推导，记作 。

   • （基础情况）

   • 若 且 ，则 （归纳情况）

3. 从起始符号推导得出的任意符号串称为句型（sentential form）。 是一个句型当且仅当 。

   • 不含有非终结符的句型称为句子（sentence）。

4. 最左推导（leftmost derivations） ：如果 是由终结符构成的字符串，且 是一个推导式。称 为一个最左推导 。定义 表示 可以通过零步或者若干步最左推导 变成 。

5. 最右推导（rightmost derivations） ：我们称 是一个最右推导，如果 是由终结符构成的字符串，且 是一个推导式。定义 表示 可以通过零步或者若干步最右推导 变成 。

6. 推导是一个建立语法分析树的过程。

7. 语法分析树（Parse Tree / Syntax Tree）是一棵用某个特定的上下文无关文法中的符号对每个结点做标记的树：

   • 叶子结点：用终结符或者 标记；

   • 中间结点：用非终结符标记；

     • 子结点用父结点的推导式体中的符号标记；

   • 根结点：用起始符号标记。

8. 语法分析树的产出（yield）：按照前序遍历的顺序将叶子结点上的记号拼接起来得到的字符串称为语法分析树的产出 。

   例子：产生式为 ， 产出 5 + ( 1 * 12 ) 的一棵语法分析树。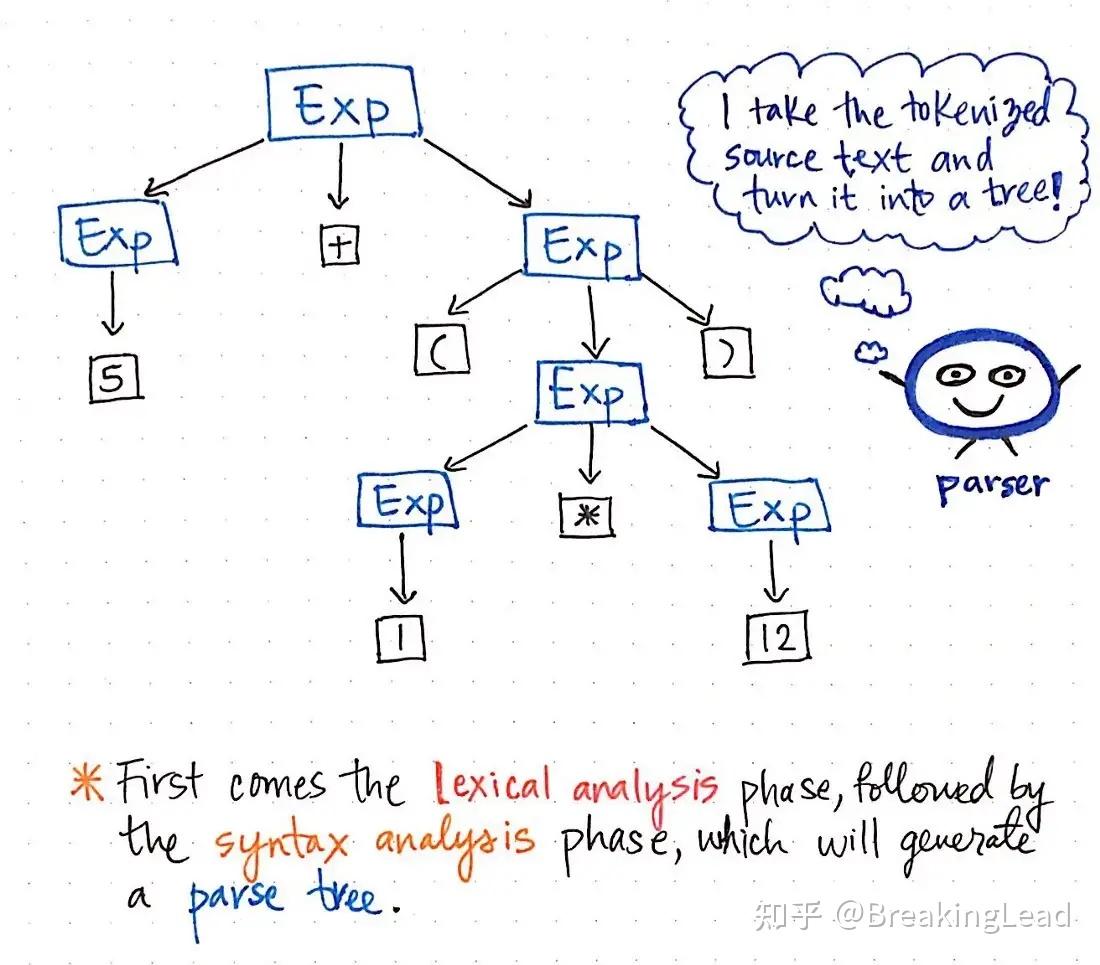

   

1.1.4 歧义

1.1.4.1 文法歧义

• 一个上下文无关文法是有歧义的（ambiguous） ，如果在这个文法定义的语言中，存在一个字符串，它可以由两个或者更多的解析树产出。

• 文法歧义的例子：

  

• 如果存在两个不同的解析树，就一定存在两种不同的最左推导方式，也就一定存在两种不同的最右推导方式。

• 对于歧义（Ambiguity）的理解：

  • 一定要注意“歧义”说的是文法的性质，并不是语言的性质。
  • 文法可以看做描述语言的方法，文法的歧义说的是描述一个语言的方法不唯一，例如上例中有两种不同的语法树，但是无论哪一种语法树，其描述的对象——合法的算术表达式这一语言，是没有歧义的。
  • 事实上，我们已经提到过，一个合法的CFG能确定一个上下文无关语言，所以只要能写出合法CFG，其语言都是没有歧义的。所谓具有固有歧义的语言，说的也是描述这个语言的文法的歧义是固有的、不可消除的。

1.1.4.2 消除歧义

• 我们通常不希望文法有歧义。有时候，只要对文法进行一些简单的改写，就能消除文法的歧义。
• 例1：提升特定运算符的优先级。
  • 有歧义:
  • 无歧义:
• 例2：提升已匹配的语句的优先级。
  • 龙书（龙书三） 4.3.2节
• 其实文法有歧义也并非多大的问题，一些现代的语法分析算法（如：优先级上升算法）在一定程度上允许歧义文法的使用。

1.1.4.3 固有歧义

• 有时候我们可以轻松地将二义性文法改写成无二义性的，那么对于所有上下文无关语言，其文法的歧义都可以通过改写来消除吗？

  答案是——不能。

• 有些上下文无关语言无论怎么改写文法都有歧义，这种只有有歧义文法的语言称为先天二义性的语言（Inherently ambiguous Language）。例如： 。

• 事实上并没有一个通用的能消除歧义的算法，甚至连判定一个文法是否是歧义文法的算法都不存在。

1.1.5 乔姆斯基范式

• 之前的CFG定义里面，我们没有对产生式体做任何要求，这使得我们可以写出既有终结符又有非终结符的很复杂的产生式体。这样生成的语法分析树也是一棵多叉树。有没有办法对产生式做一些等价变换的操作，使得产生式体更加优雅？

• 1956年，语言学家乔姆斯基证明了所有上下文无关语言（Context-Free Language, CFL）都可以用乔姆斯基范式（Chomsky Normal Form, CNF）表示。

• 称一个上下文无关文法符合 乔姆斯基范式（Chomsky Normal Form，CNF） ，如果每个产生式都满足下面两种形式的其中一种：

  1. （产生式体是两个变量）；

  2. （产生式体是一个终结符）。

• 符合乔姆斯基范式的文法生成的语法分析树是一棵二叉树，这为我们研究CFL的性质提供了便利。

1.2 下推自动机（PDA）

• RE 在定义语言的能力上和 NFA / DFA 等价，RE 是代数视角，DFA / NFA 则是自动机视角。
• CFG 定义了一种语言，并且 CFG 是代数视角的，那么直觉上应该有一种自动机能在语言定义能力上和 CFG 等价。
• 这就是下推自动机（Pushdown Automata，PDA）。
  • 下推自动机直观上来说就是NFA + 一个栈，在NFA的基础上额外允许一个栈操作。
  • PDA有确定性下推自动机（Determinstic Pushdown Automata，DPDA）也有非确定性下推自动机（Nondeterminstic Pushdown Automata，NPDA），只有NPDA才能定义所有的上下文无关语言。
  • PDA不加任何定语时，默认是NPDA，

1.2.1 形式化定义

这还是一个声明式定义

• 定义一个 下推自动机（Pushdown Automata） 为一个七元组 ，其中：

  • 是一个有限的 状态(state) 的集合；

  • 是一个 输入字母表(input alphabet) ；

  • 一个 栈字母表(stack alphabet) ；

  • 是一个 转移函数(transition function) ；

    • 转移函数接收3个参数：

      • 一个状态 ；

      • 一个输入 或者 ；

      • 一个栈符号 ；

    • ，可能是空集；

    • 如果 ，那么PDA可以在状态 ，接收输入 ，并且观察到栈顶元素为 的时候：

      • 状态变为 ；

      • 从输入的首部接收一个字符 ， 可能是 ；

      • 将栈顶的元素 替换成序列 。

  • 是一个 起始状态(start state) ， ；

  • 是一个 起始符号(start symbol) ， ； (初始的时候栈里面只有栈顶一个符号, 就是初始符号)

  • 是一个 终止状态(final states) 的集合 ， 。

• 符号约定：

  • 是输入符号；

    • 允许 作为输入符号；(-NFA)

  • 是栈符号；

  • 是输入符号形成的字符串；

  • 是栈符号形成的字符串。

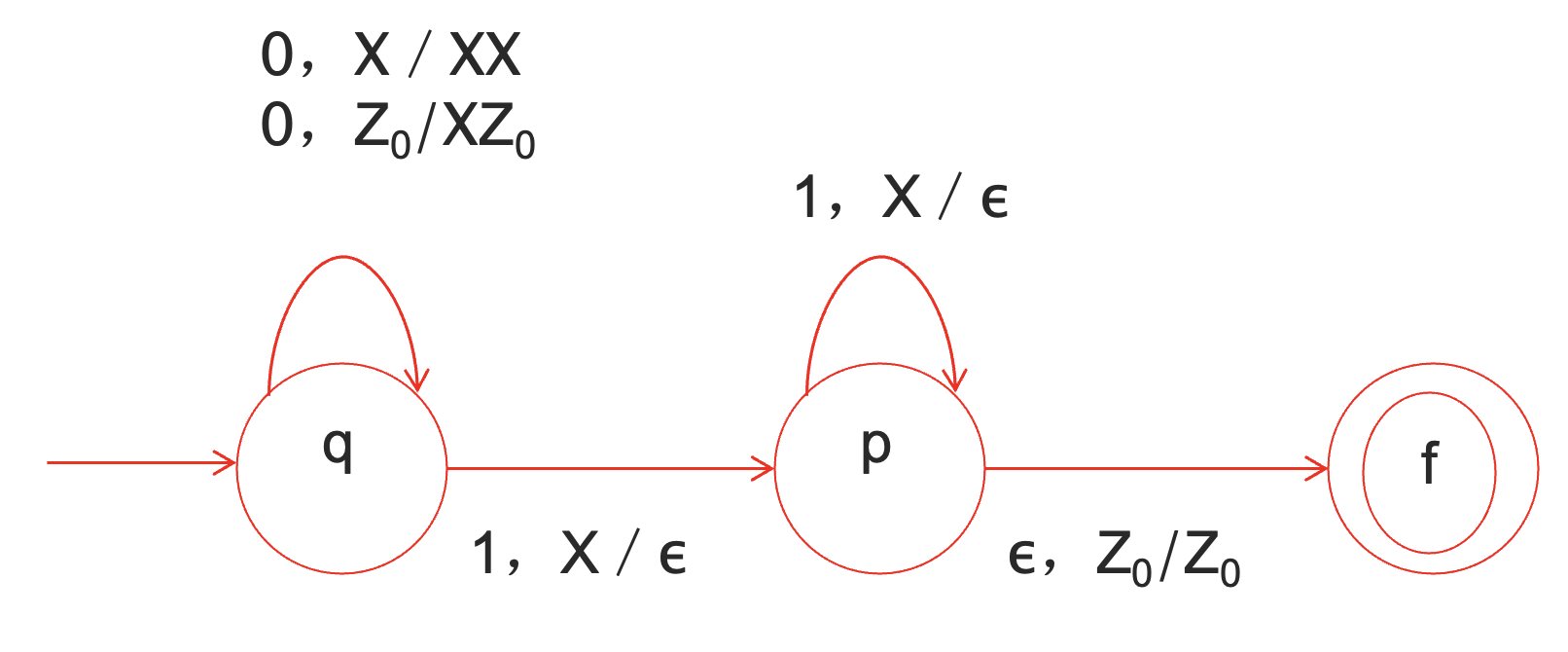
• 例子：识别 的PDA

  • 表示弹出栈顶的 , 压入串 .

  

1.2.2 即时描述

• 想要形式化地描述某个时刻PDA的状态，应该如何实现？
• 一个 即时描述(Instantaneous Description, ID) 是一个三元组 ，其中：

  1. 是当前状态；

  2. 是剩余的输入；

  3. 是栈的内容，左侧为栈顶。

• 一个 ID 可以简单理解为快照，ID也可以认为是广义的“状态”。
• 如果ID 可以通过PDA的一步移动变成ID ，我们写作
  • 零或若干步移动写作：

1.2.3 PDA的语言

• 目前只给出了PDA的定义，那么我们如何利用PDA去定义一个语言？

• 方式一：根据终止状态定义。

  若 是一个PDA，定义

• 方式二：根据空栈定义。

  若 是一个PDA，定义

• 定理： 与 在定义语言的能力上是等价的。

  • 注意，并不是对于同一个， = ，而是他们定义的语言的集合相同。
  • 证明：只要证明二者可以互相模拟对方即可。
    • ：用空栈接受模拟终止状态接受。在终止状态后增加一个擦除状态保证最终栈会为空，此外还要在初始时压入一个特殊的栈底标记以避免转移过程中意外空栈。
    • ：用终止状态接受模拟空栈接受。初始时压入特殊栈底符号，后续如果发现读到则意味着到达原来的空栈状态，此时终止即可。

• 确定性下推自动机（Determinstic Pushdown Automata, DPDA） ，对于任意状态 ，输入符号 以及栈符号 ，最多只有一种移动的选择（也不能有转移）。

• 与NFA和DFA等价不同的是，NPDA要比DPDA在表达能力上更强一些，并且是严格地更强。能够使用DPDA定义的语言有一个无歧义的文法（反过来不成立），但是NPDA定义的语言可以是有固有的歧义的。

• NPDA表达能力更强，但是仅仅是理论模型，并不能直接实现；DPDA才是可实现的，可用于解析器的建模。

1.2.4 与CFG的等价性

1.2.4.1 基本思想

构造性证明，只要构造两者之间互相转换的算法即可。

1.2.4.2 证明（选学）

本节仍是抄的《形式语言与自动机》...

1. CFG转化成PDA

   对于CFG ，令 ，构造PDA 使得 。

   其中， 有：

   • 一个状态 ；

   • 输入符号是 的终结符；

   • 栈符号是 中的所有符号；

   • 起始符号是 的起始符号。( 即 S )

   直觉上， 的每一步应该代表某个 左句型(Left-Sentential Form, LSF) ，即最左推导中的一步。

   如果 的栈是 且 到目前为止消耗了输入中的 ，那么此刻的 应该代表左句型 。

   这样的话，到达空栈的时候，被消耗的输入就是 中的一个字符串了。

   具体地， 的转移函数如下：

   1. • 这个步骤并没有改变 表示的左句型，但是将提供 的责任从栈转移到输入上了。

   2. 如果 是 的一个产生式，则

      • 猜测即将使用的 的一个产生式，并且表示推导中的下一个左句型。

   下面证明 。

   我们先证明

   先证充分性。对 使用的步骤数进行归纳。

   基础情况：0步，则 ，并且 永真。

   归纳：考虑 的 次移动， ，并且假设结论对于 次移动的情况都成立。

   有两种情况需要考虑，取决于最后一次移动是用的第一条规则还是第二条规则。

   • 如果使用第一条规则，则移动序列一定形如 ，其中 。

     • 根据归纳假设，对于前 步，有 ，而 ，则 。

   • 如果使用第二条规则，则移动序列一定形如 ，其中 是一个产生式，且 。

     • 根据归纳假设，对于前 步，有 ，又 ，从而 。

   再证必要性，对最左推导中的步骤数进行归纳，想法是类似的，这里就不再重复了。

   现在，我们已经有了对于任意的 ， 当且仅当 。

   特别地，令 ，那么 当且仅当 ，也就是说 当且仅当 ，即 。

2. PDA转化成CFG

   现在，假设 ，我们下面将会构造一个上下文无关文法 使得 。

   直观来讲， 当中会存在变量 用于产生一系列输入，这些输入能够使得 从状态 开始，弹出栈符号 ，然后转到状态 。

   • 在这个过程中栈顶不会走到 下面。（栈可以进行任何的变化, 但是不能变到X以下，并且产生的一个净效果是会在最后刚好把X弹出，过程中栈没有走到X以下。）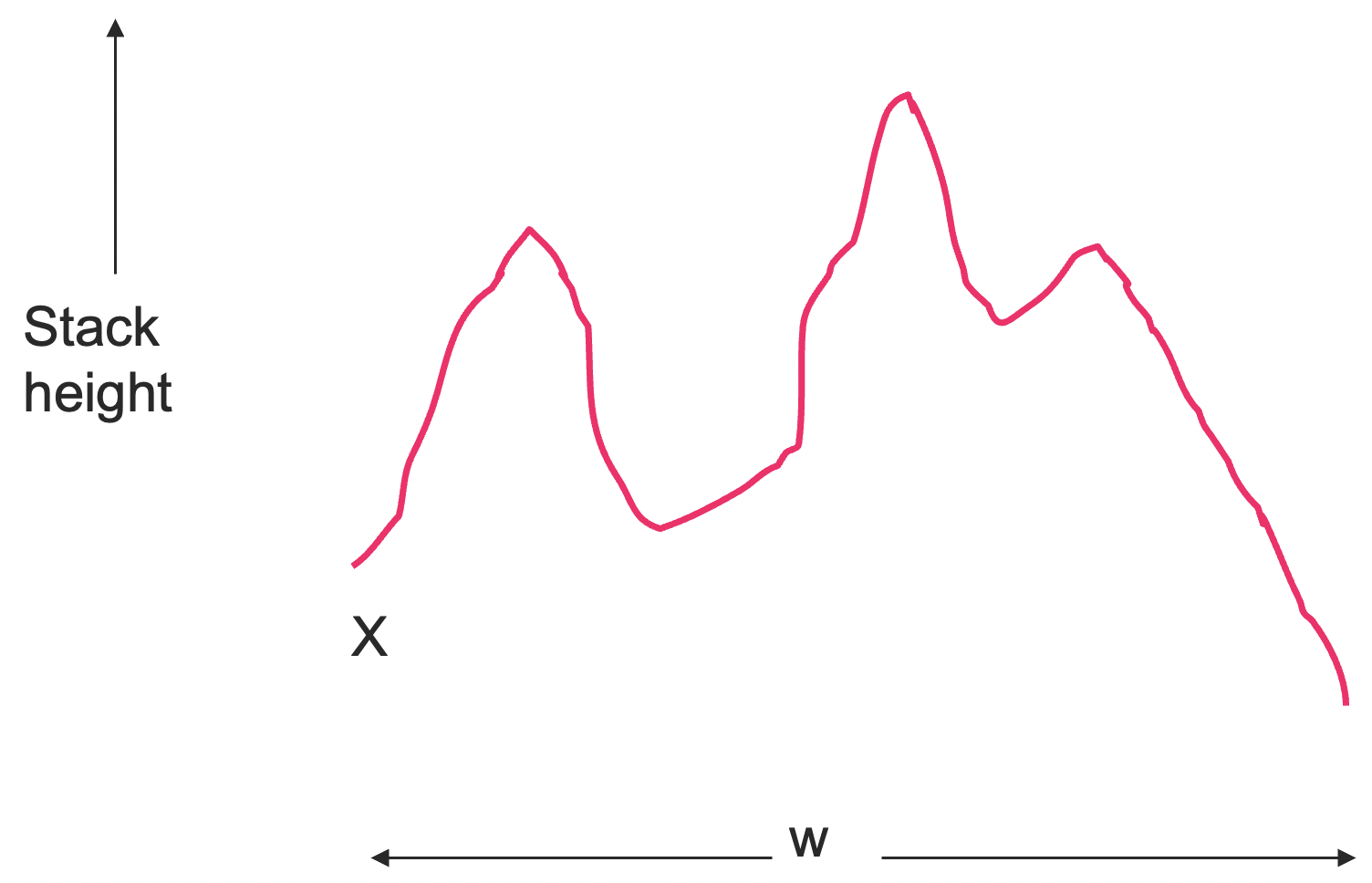

     

   下面进行形式化的构造。

   中的变量都形如 ，这个变量产生且仅产生使得 的字符串。再次之外还有一个起始符号，我们将之后讨论。

   对于 的每一个产生式都来源于 中在状态 栈顶元素 的情况下的移动情况。

   最简单的情况： 。

   • 注意， 可以是一个输入符号，也可能是 。

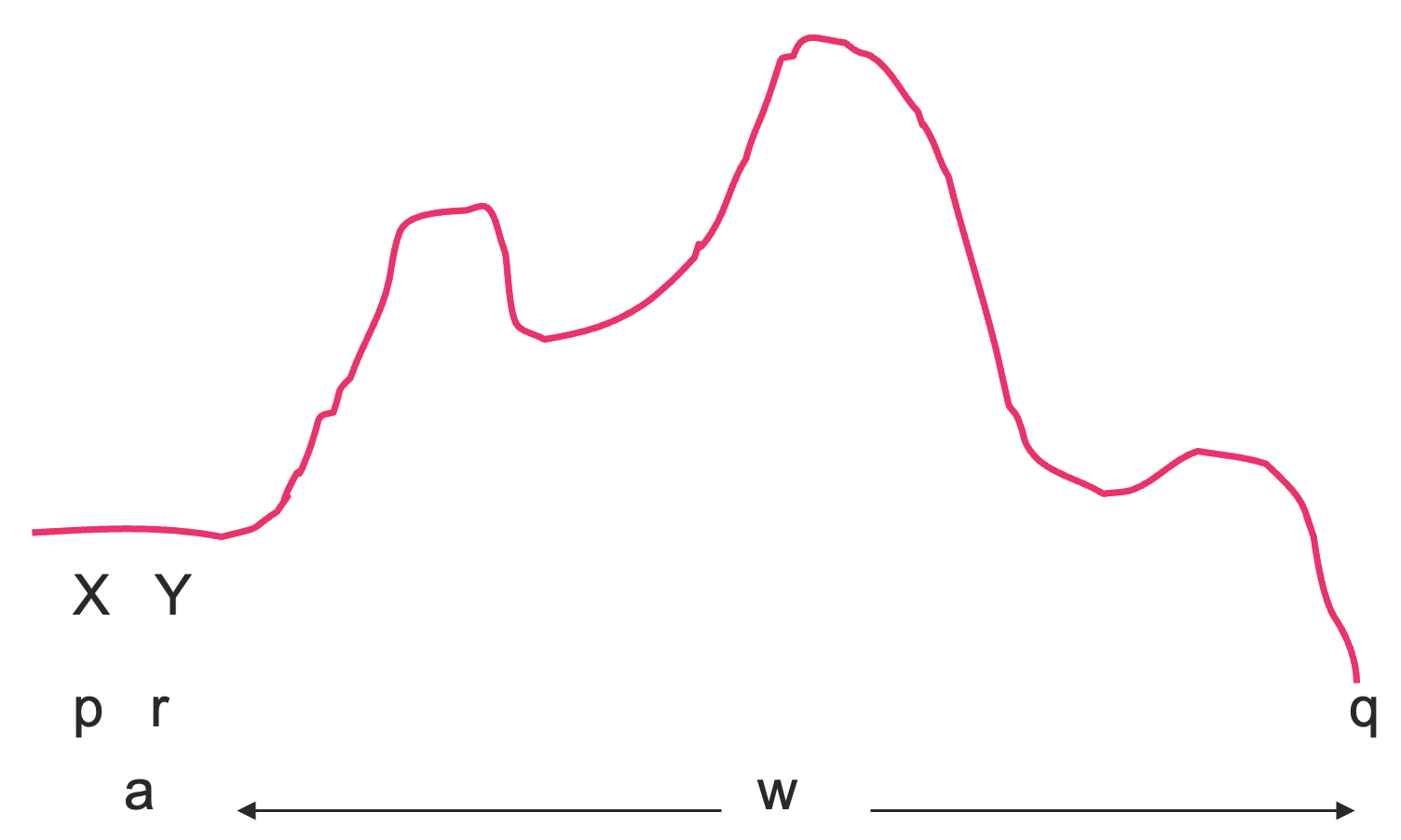
   这样的话，对应的产生式就是 。这里， 产生 ，因为读取 是弹出 并从 走到 的一种方式。

   下一种最简单的情况：对于某个状态 和符号 ， 。

   在这种情况下， 有产生式 。

   • 我们可以我们可以擦除 并从 走到 ，通过先读一个 ，进入状态 且用 代替 ，然后再读取某个字符串 ，让 从 走到 ，并移除 。 （不必担心 a[rYq] 能不能形成有效的产生式, 大不了后面还可以用各种方式处理文法（形成乔姆斯基范式））

   

   第三种最简单的情况是：对于某个状态 和符号 ，有 。

   现在， 用 代替了 ，为了删除 ， 需要先删除 ，从状态 走到某个状态 ，然后删除 ，从状态 走到状态 。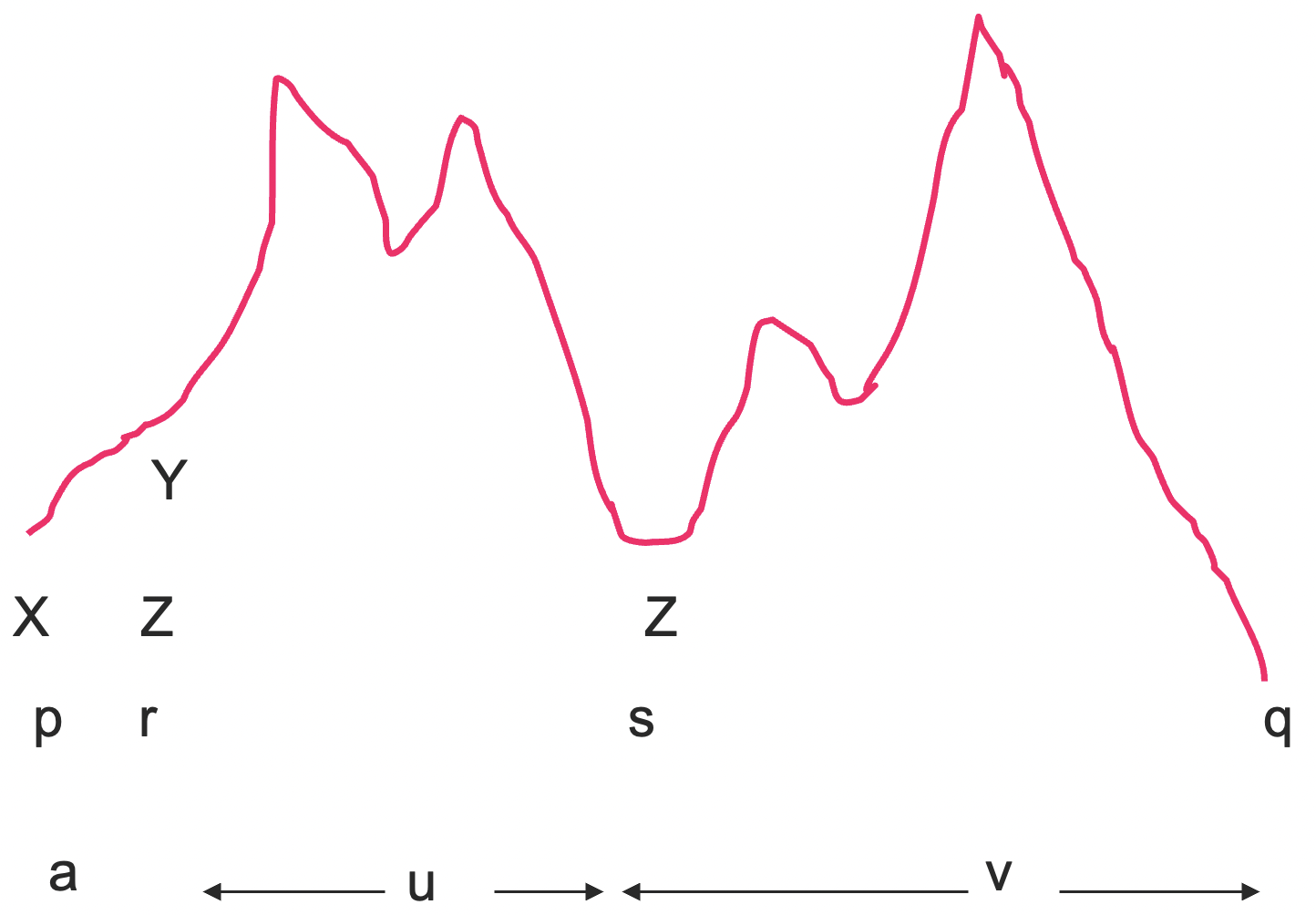

   

   由于我们并不知道中间状态 到底是什么（非确定性），我们必须对每一种可能的状态 (中继状态是什么没有限定!)，生成一个产生式 。

   这样， 其中 且 。

   经过了三个简单情况的讨论，我们可以总结一下一般的情况了。

   假设对于某个状态 以及 ，存在 ，生成

   最后我们来完成一下整个构造。我们可以证明 当且仅当 。

   • 证明方法是两个简单的归纳，这里就不再证了。

   不过，状态 可以是任何一个状态，因为我们求的是 。( 只要栈为空, "终止状态" 是什么都无所谓. )

   最后，在 中加入另一个变量 ，作为起始符号，并且对每一个状态 ，添加产生式 。

1.3 上下文无关语言

• 由CFG或NPDA定义的语言就是上下文无关语言（CFL）。

1.3.1 封闭性

封闭性指的是给定某个语言类的一些语言，对于这些语言进行某个操作得到的另一个语言依旧在同一个语言类中。

对于CFL，以下操作是封闭的：

• 并集
• 拼接
• 星闭包
• 翻转

在以下操作下，CFL不封闭：

• 交集， 是CFL， 也是CFL，但 不是CFL（证明见下一节）。
• 差集，由于 ，交集不封闭，则差集不封闭。
• 补集，考虑德摩根律。

1.3.2 泵引理

• 上下文无关语言的泵引理（Pumping Lemma）：

  对于每一个上下文无关语言 ，存在一个整数 （泵引理常数） ，使得 ， ，满足：

  • ；

  • ；

  • 。

• 直观理解：从语法分析树的视角，乔姆斯基范式的文法产生一棵语法分析树是二叉树，假设其有m个非终结符，那么如果语法分析树上的每条路径都不使用重复的非终结符，则生成的串的长度一定有限，一旦这个语言中有一个串的长度超过了这个极限（泵引理常数），那么就一定有路径上重复出现了相同的非终结符，这样，由于文法是上下文无关的，我们能将两个相同的非终结符中间的部分不断重复若干次，这生成的串仍符合语法，如此就达到了源源不断“泵”出字符串的效果。

• 例子：

  • 不是上下文无关语言。

    证明：假设 是一个上下文无关语言，令 是 的泵引理常数。

    考虑 ，我们可以写作 ，其中 且 。

    第一种情况： 中没有 。

    • 它们之中至少有一个是 ，从而 中至多有一个 ，这是不可能的，因为这样 就 了。

    第二种情况： 至少有一个 。

    • 的长度太短了（ ），从而无法覆盖 中所有的三个 字串。(如果要覆盖到3段的0, 长度至少要n + 4, 但是 vwx 长度 <= n)

    • 于是， 中至少有一个 子串 (没有被 覆盖到)，以及至少一个 字串不足 个 （因为 删去而被丢掉了）。

    • 从而， 。

  • 不是上下文无关语言。

    证明思路：考虑泵引理常数，则 最多覆盖 的两个元素，那么使用泵引理时一定至少覆盖到一个元素，至少没覆盖到一个元素，使用泵引理后，这两者的数量一定不相等。

1.3.3 成员资格问题

任意给定一个字符串和CFG, 是否满足这个CFG？（语法分析）

1.3.3.1 构造NPDA

将CFG转换成NPDA，再检查NPDA是否接受。

• 这个算法很直观，并且是通用的，可以处理所有的CFG。我们的计算机是图灵完备的，因此可以模拟NPDA的运行。
• 但是这个算法也只有理论价值，因为它的复杂性是指数级的，过于高。

1.3.3.2 CYK算法

• CYK（Coke-Younger-Kasami）算法是以三位科学家的名字首字母命名的，它也是通用的，可以处理所有CFG。
• 并且它相对NPDA要高效得多，在时间内即可判断一个字符串是否满足某CFG。

1.3.3.3 LL / LR语法分析算法

• 尽管CYK算法相对高效，但是在实际编译器设计中并不使用，因为的开销还是太大了。并且实际上也并不需要追求语法分析算法的通用性。
• 例如，LL(1) 文法是一种极其特殊的CFG，但是如果源语言的文法是LL(1)文法，我们就能轻松地使用 时间复杂度的 LL(1) 语法分析算法来完成语法分析。

下面将详细介绍各种常用的语法分析算法。

---

2 LL语法分析

• 语法分析：
  • 输入
  • 输出
• L ？ L？

3 优先级上升语法分析

4 LR语法分析 (选学)

5 ANTLR 4 语法分析